今回の記事では、ダランベールの原理について解説していきます。
ダランベールの原理とは
ダランベールの原理とは、仮想仕事の原理を拡張したものです。
運動方程式を力のつりあいの式と同じにすることで、動力学を静力学に帰着させることができるというとても便利な法則です。つまり、運動している物体を静止している物体と同じように扱えます。
ダランベールの原理の式は以下の通りです。
$$(F-m\ddot{r})\cdot \ δr=0$$
ダランベールの原理の導出
1個の質点の運動
ここからは、ダランベールの原理を導いていきます。まずは、等加速度運動をしている1個の質点の運動方程式を考えます。
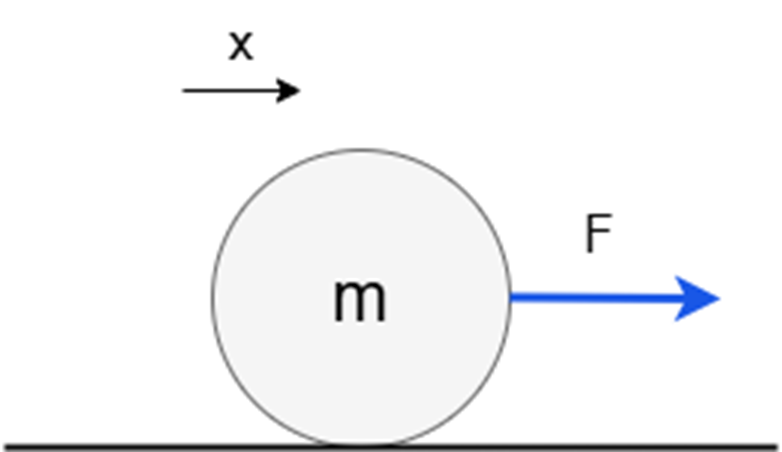
上の図の質点の運動方程式はもちろん
$$F=m\ddot{x}$$
ですね。ここで、両辺を左辺に集めると
$$F-m\ddot{x}=0$$
となります。このとき
$$-m\ddot{x}$$
を質点に作用する1つの力(慣性力)であるとみなすと、図に表すと以下のようになります。
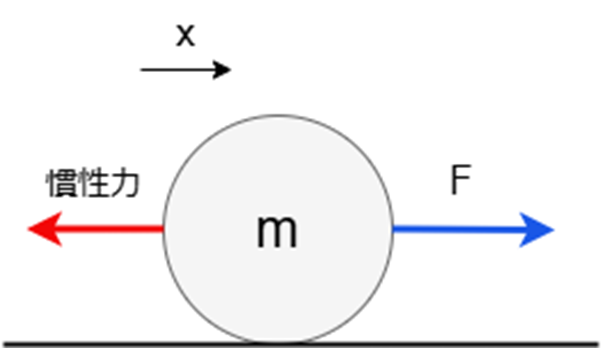
これで運動方程式を、力のつりあいで考えることができるようになりました。
三次元に拡張する
次に、これを一般化するために3次元デカルト座標(空間)で考えます。この空間座標での、ある質点の位置ベクトルを$r$とおくと
$$F-m\ddot{r}=0 \quad (1)$$
と表すことができます。ここで、仮想仕事の原理を使います。
$$δW=F\cdotδr=0$$
仮想仕事の原理の詳しい説明については以下の記事を参照してください。

(1)の式に仮想仕事の原理を適用すると
$$δW=(F-m\ddot{r})\cdot \ δr=0 \quad (2)$$
となり、ダランベールの原理の式を導くことができました。
ダランベールの原理からニュートンの運動方程式を得る
(2)の式をさらに変形していきます。(2)の式のベクトルをそれぞれ成分表示することで
$$\delta W=(F_x-m\frac{d^2 x}{dt^2})\delta x+(F_y-m\frac{d^2 y}{dt^2})\delta y$$
$$+(F_z-m\frac{d^2 z}{dt^2})\delta z\quad (3)$$
ここで、ラグランジュの未定乗数法に近い操作を行います。
束縛条件として
$$f(x,y,z)=0$$
を考えると、この全微分は
$$df=\frac{\delta f}{\delta x}dx+\frac{\delta f}{\delta y}dy+\frac{\delta f}{\delta z}dz=0$$
これに未定乗数$\lambda$をかけて(3)の辺々に足し合わせます。
$$\delta W=(F_x-m\frac{d^2 x}{dt^2}+\lambda \frac{\delta f}{\delta x})\delta x$$
$$+(F_y-m\frac{d^2 y}{dt^2}+\lambda \frac{\delta f}{\delta y})\delta y$$
$$+(F_z-m\frac{d^2 z}{dt^2}+\lambda \frac{\delta f}{\delta z})\delta z$$
この仮想仕事$\delta W$は、任意の方向の変位$\delta x,\delta y,\delta z$に対して、0とならなければいけません。よってxについてのみ考えると
$$F_x-m\frac{d^2 x}{dt^2}+\lambda \frac{\delta f}{\delta x}$$
となり、この式を移項することによって
$$m\frac{d^2 x}{dt^2}=F_x+\lambda \frac{\delta f}{\delta x}$$
となり、これが$y,z$も同様に成立するので、ニュートンの運動方程式と同等のものが得られたことになります。
まとめ
今回は、ダランベールの原理について解説しました。ダランベールの原理は、ラグランジュの運動方程式の導出にも使えるとても重要な法則です(かなり長いので今回の記事では省略しました)。しっかり理解しておきましょう。


