今回の記事では積分方程式について解説していきます。
ラプラス変換を使って積分方程式を解く
ラプラス変換を使って積分方程式を解くときも、微分方程式をラプラス変換を使って解くのと同じ要領で計算することができます。微分方程式のラプラス変換を使って解くやり方については以下の記事を参照してください。

積分方程式はラプラス変換を利用することで以下の図のイメージで解くことができます。
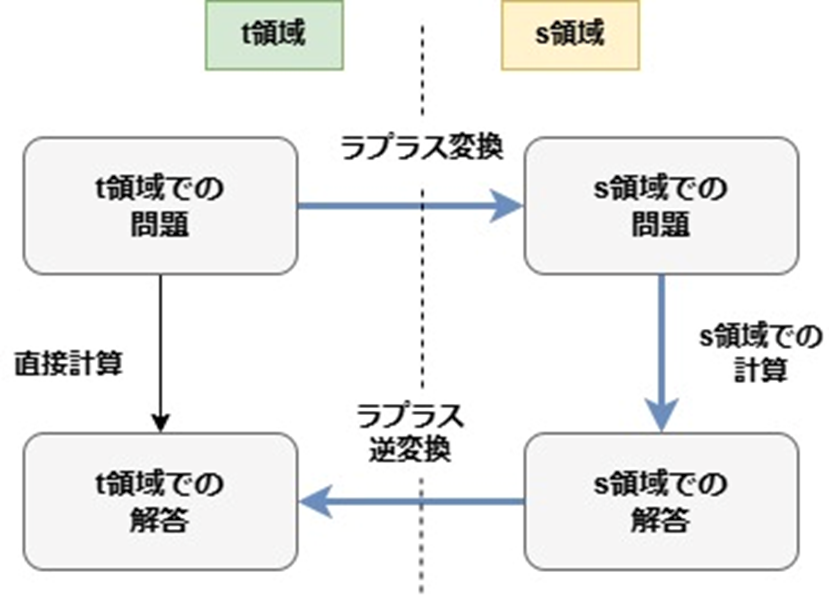
ラプラス変換を使って積分方程式を解く4STEP
積分方程式はラプラス変換を使って以下の4STEPで解くことができます。
積分方程式の両辺にラプラス変換を行い、s領域にします。
$L[y]=Y$とおいた後、積分部分をたたみ込みの式に変形し、これを先ほど両辺にラプラス変換を行った式に代入します。
$Y=~$の形にします。このとき右辺は逆ラプラス変換しやすい形にしておきます。
両辺を逆ラプラス変換します。$L[y]=Y$とおいたので、これでyが求めることができます。
例題
この4STEPを使って例題にチャレンジしてみましょう。
【例題(1)】$y=1+\int_{0}^{t} (t-u)y(u)du$をラプラス変換を使って求めよ
まずは与式の両辺をラプラス変換します。すると
$$L[y]=L[1]+L[\int_{0}^{t} (t-u)y(u)du]$$
$L[y]=Y$とする。ここでたたみ込みの定義より$f(t) \ast g(t)=\int_{0}^{t}f(t-u)g(u)du \quad (t \gt 0)$なので、このとき$f(t)=t$,$g(t)=y$である。したがって
\begin{eqnarray}Y=& &\frac{1}{s}+L[t\ast y]\\& &=\frac{1}{s}+L[t]・L[y]\\& &=\frac{1}{s}+\frac{1}{s^2}・Y \end{eqnarray}
途中の計算には$L[f(t)\ast g(t)]=L[f(t)]L[g(t)]$を利用しました。
$$(1-\frac{1}{s^2})Y=\frac{1}{s}$$
$$Y=\frac{s}{s^2-1}$$
部分分数分解を利用することで
$$Y=\frac{1}{2}(\frac{1}{s-1}+\frac{1}{s+1})$$
ここで両辺を逆ラプラス変換することによって
$$y=\frac{1}{2}e^t+\frac{1}{2}e^{-t}$$
これで積分方程式を解くことができました。
練習問題
練習問題にチャレンジしてみましょう。
$y=2t+\int_{0}^{t} \sin{(t-u)}y(u)du$をラプラス変換を使って求めよ
まずは与式の両辺をラプラス変換します。
$L[y]=L[2t]+L[\int_{0}^{t} \sin{(t-u)}y(u)du]$
$L[y]=Y$とする。ここでたたみ込みの定義より$f(t) \ast g(t)=\int_{0}^{t}f(t-u)g(u)du \quad (t \gt 0)$なので、このとき$f(t)=\sin{t}$,$g(t)=y$である。したがって
\begin{eqnarray} Y& &=\frac{2}{s^2}+L[\sin{t} \ast y]\\& &=\frac{2}{s^2}+L[\sin{t}]・L[y]\\& &=\frac{2}{s^2}+\frac{1}{s^2+1}・Y \end{eqnarray}
途中の計算には$L[f(t)\ast g(t)]=L[f(t)]L[g(t)]$を利用しました。
$$(1-\frac{1}{s^2+1})Y=\frac{2}{s^2}$$
$$Y=\frac{2}{s^2}+\frac{2}{s^4}$$
ここで両辺を逆ラプラス変換することによって
$$y=2t+\frac{1}{3} t^3$$
これで積分方程式を解くことができました。
まとめ
今回は積分方程式をラプラス変換で解く方法について解説しました。たたみ込みが利用できそうな積分方程式はラプラス変換を利用できるようにしておきましょう。


