今回の記事では、ハミルトニアンとハミルトンの運動方程式(ハミルトンの正準方程式)について解説していきます。
ハミルトン形式(正準形式)
ラグランジアン$L(q(t),\dot{q}(t),t)$と最小作用の原理を基本とする形式をラグランジュ形式というのに対し、一般化座標と$q$と一般化運動量$p$を基本とする形式をハミルトン形式(正準形式)といいます。ラグランジュ形式における、ラグランジアンはハミルトニアン、オイラー・ラグランジュ方程式はハミルトンの運動方程式(ハミルトンの正準方程式)に対応します。
ハミルトン形式の有用性は、特に正準変換の時に現れます。
ハミルトニアンとは
ハミルトニアンは、一般化座標$q$と一般化運動量$p$を用いて以下のように定義されます。
ある物体系のハミルトニアン$H(q,p,t)$は
$$H=\displaystyle \sum_{i=1}^n p_i \dot{q_i}-L$$
ハミルトニアンの意味
ハミルトニアン$H(q,p,t)$の物理的な意味は、「系のエネルギー$E$」です。厳密にいえば、もっと広い概念ですが、多くの場合でハミルトニアンはエネルギーとして扱います。
ハミルトニアンをエネルギーとして扱わないものの一例として、「ハミルトン・ヤコビ方程式」があります。ハミルトン・ヤコビ方程式では、ハミルトニアンを$0$だと考えるという、エネルギーとしてはありえない考え方をします。
ハミルトンの運動方程式(ハミルトンの正準方程式)とは
ハミルトニアン$H(q,p,t)$の系における、ハミルトンの運動方程式(ハミルトンの正準方程式)は以下のような式です。
$$\dot{q}_i=\frac{\partial H}{\partial p_i}, \quad \dot{p}_i=-\frac{\partial H}{\partial q_i}$$
この2つの方程式を合わせてハミルトンの運動方程式といいます。
ハミルトニアンの保存
ハミルトニアンが時間に陽に依存しないとき、ハミルトニアンの量は保存します。このことを式で表すと以下のようになります。
$$\frac{d}{dt}H(q(t),p(t))=0$$
ハミルトニアンが時間に陽に依存しないとはどういうことか、詳しく説明します。ハミルトニアンは先に示した通り、$q(t),p(t),t$の3つの関数で表されます。
このハミルトニアンがtの関数を直接持たないとき、つまり$q(t),p(t)$のみで表されるときを時間に陽に依存しないといいます。
練習問題
以下の練習問題はオイラー・ラグランジュ方程式の記事と同じ問題です。ハミルトンの運動方程式を求めて、オイラー・ラグランジュ方程式と一致するかどうか確かめてみましょう。
【練習問題 1】自由落下
一様な重力場の下、自由落下している質量mの質点の運動を考える。
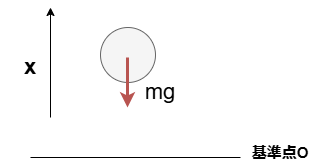
(1)位置を$x(t)$としてハミルトニアンを求めよ。
(2)この系のハミルトンの運動方程式を求めよ。
【解答】
(1) この系において
$$T=\frac{1}{2}m\dot {x}^2, \quad U=mgx$$
なので、ラグランジアンの式$L=T-U$より
$$L=\frac{1}{2}m\dot {x}^2-mgx$$
ここで位置$x$に対応した($x$に共役の)運動量$p$は
$$p=\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$
これを$x$について解いて
$$\dot{x}=\frac{p}{m}$$
よってハミルトニアンの式$H=\displaystyle \sum_{i=1}^n p_i \dot{q_i}-L$より
\begin{eqnarray} H& &=p\dot{x}-L\\& &=\frac{p^2}{m}-\{\frac{1}{2}m\left(\frac{p}{m}\right)^2-mgx\}\\& &=\frac{p^2}{2m}+mgx \end{eqnarray}
(2) $H=\frac{p^2}{2m}+mgx$より、ハミルトンの運動方程式を考えます。
$$\frac{\partial H}{\partial x}=mg$$
$$\frac{\partial H}{\partial p}=\frac{p}{m}$$
これをハミルトンの運動方程式$\dot{q}_i=\frac{\partial H}{\partial p_i}, \quad \dot{p}_i=-\frac{\partial H}{\partial q_i}$に代入します。
\begin{cases} \dot{x}=\frac{p}{m} \quad (1)\\ \dot{p}=mg \quad (2) \end{cases}
これでハミルトンの運動方程式を求めることができました。これがオイラー・ラグランジュ方程式と一致することを確かめてみましょう。
(1)式より$p=m\dot{x}$であり、この式を(2)式に代入すると
$$\frac{d}{dt}(m\dot{x})=-mg$$
$$m\ddot{x}=-mg$$
これでオイラー・ラグランジュ方程式と一致しました。
【練習問題 2】単振り子
振動している単振り子がある。このとき棒の先につけた質量mの質点の運動を考える。ただし棒は伸縮せず質量はないものとする。
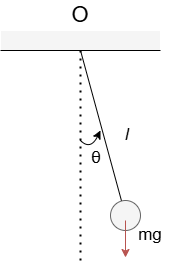
(1)棒が鉛直線となす角度を$\theta (t)$としてハミルトニアンを求めよ。
(2)この系のハミルトンの運動方程式を求めよ。
【解答】
(1) 単振り子の重りの速さは$v=l\dot {\theta}$です。ここで単振り子の最下点を基準点($U=0$)とすると、この系において
$$T=\frac{1}{2}ml^2 \dot {\theta}^2, \quad U=mgl(1-cos{\theta} )$$
なので、ラグランジアンの式$L=T-U$より
$$L=\frac{1}{2}ml^2 \dot {\theta}^2-mgl(1-cos{\theta} )$$
ここで角度$\theta$に対応した($\theta$に共役の)運動量$p$は
$$p=\frac{\partial L}{\partial \dot{\theta}}=ml^2 \dot{\theta}$$
これを$\theta$について解いて
$$\dot{\theta}=\frac{p}{ml^2}$$
よってハミルトニアンの式$H=\displaystyle \sum_{i=1}^n p_i \dot{q_i}-L$より
\begin{eqnarray} H& &=p\dot{\theta}-L\\& &=\frac{p^2}{ml^2}-\{\frac{1}{2}ml^2 \left(\frac{p}{ml^2}\right)^2-mgl(1-\cos{\theta})\}\\& &=\frac{p^2}{2ml^2}+mgl(1-\cos{\theta}) \end{eqnarray}
(2) $H=\frac{p^2}{2ml^2}+mgl(1-\cos{\theta})$より、ハミルトンの運動方程式を考えます。
$$\frac{\partial H}{\partial \theta}=mgl\sin{\theta}$$
$$\frac{\partial H}{\partial p}=\frac{p}{ml^2}$$
これをハミルトンの運動方程式$\dot{q}_i=\frac{\partial H}{\partial p_i}, \quad \dot{p}_i=-\frac{\partial H}{\partial q_i}$に代入します。
\begin{cases} \dot{\theta}=\frac{p}{ml^2} \quad (1)\\ \dot{p}=-mgl\sin{\theta} \quad (2) \end{cases}
これでハミルトンの運動方程式を求めることができました。これがオイラー・ラグランジュ方程式と一致することを確かめてみましょう。
(1)式より$p=ml^2 \dot{\theta}$であり、この式を(2)式に代入すると
$$\frac{d}{dt}(ml^2 \dot{\theta})=-mgl\sin{\theta}$$
$$ml^2 \ddot{\theta}=-mgl\sin{\theta}$$
これでオイラー・ラグランジュ方程式と一致しました。
まとめ
今回はハミルトニアンとハミルトンの運動方程式(ハミルトンの正準方程式)について解説しました。とても有用な形式なので、しっかりマスターしておきましょう。


