今回の記事では、ラプラス変換の基礎について解説していきます。
ラプラス変換とは
ラプラス変換とは、時間を表す変数tの領域からs領域に変換することです。ラプラス変換を使うことで微分方程式を簡単に解くことができます。ラプラス変換の定義式は以下の通りです。
$$L[f(t)]=F(s)=\int_{0}^{\infty}f(t)e^{-st} dt$$
ラプラス変換を使うメリット
ラプラス変換を使うメリットは大きく2つあります。
- 微分操作を文字として扱える
- 複雑なn階線形微分方程式の非同次形を簡単にすることができる
それぞれ解説していきます。
微分方程式を簡単に解ける
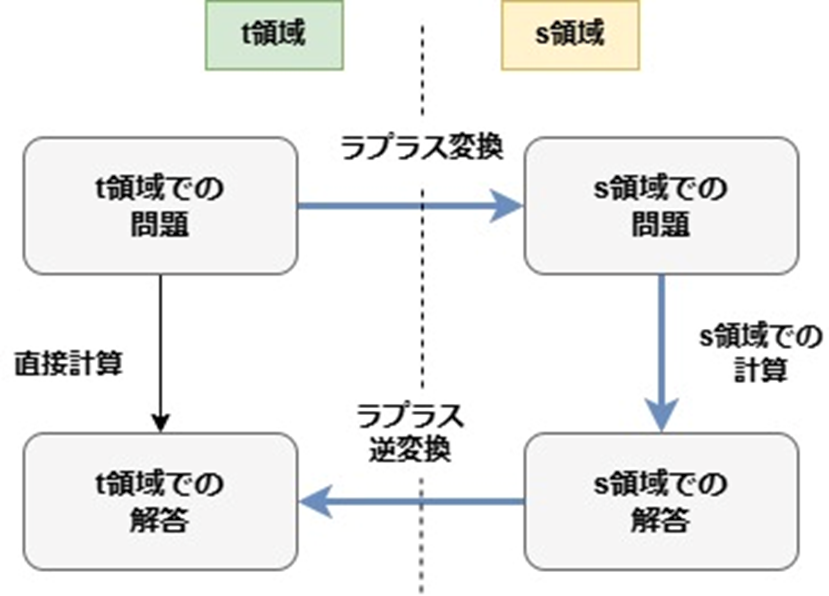
微分方程式が複雑の時に、変数変換をせず直接解くのはかなり難しいです。そこで、s領域に微分方程式を変換した後にそのs領域の中で計算します。ここで出た答えを逆ラプラス変換をすることにより、t領域での答えが出せたことになります。
微分積分が四則演算で計算できるようになる
ラプラス変換の考え方は指数対数の考え方と似ています。対数をとることのメリットは掛け算を足し算にしたり、累乗を掛け算にできることでしたね。ラプラス変換では、t領域の微分計算をsの掛け算に変え、t領域の積分計算をsの割り算に変えます。こうすることで、t領域では直接計算することが難しかった微分積分の計算が四則演算で計算できるようになるのです。
ラプラス変換で覚えるべき6つの変換
ラプラス変換で覚えるべきことはあまりありません。そこでこれだけは覚えておくべきという6つの変換を紹介します。
重要なラプラス変換
(1)$ \ L(t^n)=\frac{n!}{s^{n+1}}$
(2)$ \ L(e^{\alpha t})=\frac{1}{s-\alpha}$
(3)$ \ L{f'(t)}=sF(s)-f(0)$
(4)$ \ L({f^{\prime\prime}(t)})=s^2F(s)-sf(0)-f'(0)$
(5)$ \ L(\sin{\omega t})=\frac{\omega}{s^2+\omega^2}$
(6)$ \ L(\cos{\omega t})=\frac{s}{s^2+\omega^2}$
それぞれの証明
それぞれのラプラス変換の証明をしていきます。公式を覚えるためにも白紙に一回書いてみることをおすすめします。
(1)$\ L[t^n]=\frac{n!}{s^{n+1}}$
この公式の証明にはガンマ関数が必要になります。
$$\Gamma(n)=\int_{0}^{\infty}u^{n-1}e^{-u}du \ (n \gt 0)$$
$(1)\Gamma(n)=(n-1)!$
$(2)\Gamma(1)=1$
$(3)\Gamma(\frac{1}{2})=\sqrt{\pi}$
$(4)\Gamma(n+1)=n\Gamma(n) \ (n \gt 0)$
ラプラス変換の定義の式より計算していきます。
$$ L[t^n]=\int_{0}^{\infty}t^ne^{-st}dt$$
ここで$st=u$と置換すると、$dt=\frac{1}{s}du$であり
$$=\int_{0}^{\infty}(\frac{u}{s})^n e^{-u}・\frac{1}{s}du$$
$$=\frac{1}{s^{n+1}}\int_{0}^{\infty}u^n e^{-u}du$$
ここで積分部分を定義よりガンマに変換すると
$$=\frac{1}{s^(n+1)}\Gamma(n+1)$$
ここでガンマ関数の性質(1)を利用することで
$$=\frac{n!}{s^{n+1}}$$
(2)$ \ L[e^{\alpha t}]=\frac{1}{s-\alpha}$
\begin{eqnarray}L(e^{\alpha t})& &=\int_{0}^{\infty}e^{-\alpha t}・e^{-st}dt \\& &=\int_{0}^{\infty}e^{-(\alpha+s)t}dt\\& &=-\frac{1}{\alpha+s}\left[e^{-(\alpha+s)t}\right]_0^\infty\\& &=\frac{1}{s+\alpha} \end{eqnarray}
(3)$ \ L[f'(t)]=sF(s)-f(0)$
\begin{eqnarray}L[f'(t)]& &=\int_{0}^{\infty}f'(t)e^{-st}dt\\& &=\left[f(t)e^{-st}\right]_0^\infty +s\int_{0}^{\infty}f(t)e^{-st}dt \end{eqnarray}
途中の計算には部分積分を使いました。ここでラプラス変換の定義の式より$L[f(t)]=\int_{0}^{\infty}f(t)e^{-st}dt=F(s) $なので
$$=\displaystyle\lim_{t\to\infty}f(t)e^{-st}-f(0)+sF(s)$$
$$=sF(s)-f(0)$$
(4)$ \ L[{f^{\prime\prime}(t)}]=s^2F(s)-sf(0)-f'(0)$
\begin{eqnarray} \ L[{f^{\prime\prime}(t)}]& &=\int_{0}^{\infty}\{f'(t)\}’ e^{-st}dt\\& &= \left[f'(t)e^{-st}\right]_0^\infty +s\int_{0}^{\infty}f'(t)e^{-st}dt \\& & =\displaystyle\lim_{t\to\infty}f'(t)e^{-st}-f'(0)+s\int_{0}^{\infty}f'(t)e^{-st}dt \end{eqnarray}
$s\int_{0}^{\infty}f'(t)e^{-st}dt $の形は(3)でも出てきましたね。これを利用します。
$$=-f'(0)+s\{sF(s)-f(0)\}$$
$$=s^2F(s)-sf(0)-f'(0)$$
(5)$ \ L[\sin{\omega t}]=\frac{\omega}{s^2+\omega^2}$
オイラーの公式を利用します。
$$e^{i\omega t}=\cos{\omega t}+i\sin{\omega t}$$
オイラーの公式より$e^{i\omega t}=\cos{\omega t}+i\sin{\omega t}$、$e^{-i\omega t}=\cos{\omega t}-i\sin{\omega t}$です。これら2つの式を利用することで
$$\sin{\omega t}=\frac{e^{i\omega t}-e^{-i\omega t}}{2i}$$
となります。これに(2)の公式$ \ L[e^{\alpha t}]=\frac{1}{s-\alpha}$を利用して計算します。
\begin{eqnarray} \ L[\sin{\omega t}]& &=\frac{1}{2i}(L[e^{i\omega t}]- L[e^{-i\omega t}])\\& &=\frac{1}{2i}(\frac{1}{s-i\omega}-\frac{1}{s+i\omega})\\& &=\frac{\omega}{s^2+\omega^2} \end{eqnarray}
(6)$ \ L[\cos{\omega t}]=\frac{s}{s^2+\omega^2}$
(5)と同じ要領でやっていきます。オイラーの公式より$e^{i\omega t}=\cos{\omega t}+i\sin{\omega t}$、$e^{-i\omega t}=\cos{\omega t}-i\sin{\omega t}$です。これら2つの式を利用することで
$$\cos{\omega t}=\frac{e^{i\omega t}+e^{-i\omega t}}{2i}$$
となります。これに(2)の公式$ \ L[e^{\alpha t}]=\frac{1}{s-\alpha}$を利用して計算します。
\begin{eqnarray} \ L[\cos{\omega t}]& &=\frac{1}{2}(L[e^{i\omega t}]+ L[e^{-i\omega t}])\\& &=\frac{1}{2}(\frac{1}{s-i\omega}+\frac{1}{s+i\omega})\\& &=\frac{s}{s^2+\omega^2} \end{eqnarray}
ラプラス変換の5つの性質
ラプラス変換の性質
(1)(線形法則) $$L[af(t)+bg(t)]=aL[f(t)]+bL[g(t)]$$
(2)(相似法則) $$L[f(at)]=\frac{1}{a}F(\frac{s}{a}) \ (a \gt 0) $$
(3)(像の移動法則) $$L[ f(t)e^{\alpha t}]=F(s-\alpha)$$
(4)(微分法則) $$L[tf(t)]=-\frac{d}{ds}F(s) $$
(5)(積分法則)$$L[\int_{0}^{t}f(u) \ du]=\frac{1}{s}F(s)$$
それぞれの証明
それぞれのラプラス変換の性質の証明をしていきます。こちらも白紙に一回書いてみることをおすすめします。
(1)(線形法則) $$L[af(t)+bg(t)]=aL[f(t)]+bL[g(t)]$$
\begin{eqnarray} L[af(t)+bg(t)]& &=\int_{0}^{\infty}\{af(t)+bg(t)\}・e^{-st}dt \\& &=a\int_{0}^{\infty}f(t)e^{-st}dt+b\int_{0}^{\infty}g(t)e^{-st}dt\\& &= aL[f(t)]+bL[g(t)] \end{eqnarray}
(2)(相似法則) $$L[f(at)]=\frac{1}{a}F(\frac{s}{a}) \ (a \gt 0) $$
$$L[f(at)]=\int_{0}^{\infty}f(at)e^{-st}dt$$
ここで$at=u$と置換すると、$dt=\frac{1}{a}du$であり
$$=\int_{0}^{\infty}f(u)e^{-s・\frac{u}{a} }・\frac{1}{a}du$$
$$=\frac{1}{a}\int_{0}^{\infty}f(u)e^{-s(\frac{s}{a}) u}du$$
この式はラプラス変換の定義の式の$L[f(t)]=F(s)=\int_{0}^{\infty}f(t)e^{-st}dt=F(s) $のsが$\frac{s}{a}$になってる形なので
$$=\frac{1}{a}F(\frac{s}{a})$$
(3)(像の移動法則) $$L[ f(t)e^{\alpha t}]=F(s-\alpha)$$
\begin{eqnarray}L[ f(t)e^{\alpha t}]& &=\int_{0}^{\infty}f(t)e^{\alpha t}・e^{-st}dt\\& &=\int_{0}^{\infty}f(t)e^{-(s-\alpha) t}dt \end{eqnarray}
この式はラプラス変換の定義の式の$L[f(t)]=F(s)=\int_{0}^{\infty}f(t)e^{-st}dt=F(s) $のsが$s-\alpha$になってる形なので
$$=F(s-\alpha)$$
(4)(微分法則) $$L[tf(t)]=-\frac{d}{ds}F(s) $$
$\frac{d}{ds}F(s)$から逆算して証明していきます。
$$\frac{d}{ds}F(s)=\frac{d}{ds}\{\int_{0}^{\infty} f(t) e^{-st}dt\}$$
ここで、連続関数の微分と積分の順序は交換可能なことを利用すると
$$=\int_{0}^{\infty} \{\frac{d}{ds}e^{-st}\}f(t)dt$$
$$=\int_{0}^{\infty} -te^{-st}f(t)dt$$
$$=-\int_{0}^{\infty}(tf(t))・e^{-st}dt$$
$$=-L[tf(t)]$$
したがって
$$\ L[tf(t)]=-\frac{d}{ds}F(s) $$
(5)(積分法則)$$L[\int_{0}^{t}f(u) \ du]=\frac{1}{s}F(s)$$
$$L[\int_{0}^{t}f(u) \ du]$$
$$= \int_{0}^{\infty}(\int_{0}^{t} f(u) \ du ・e^{-st}) dt$$
$$= \left[\int_{0}^{t} f(u) \ du ・-\frac{1}{s}e^{-st} \right]_0^\infty $$
$$+\frac{1}{s}\int_{0}^{\infty}f(t)・e^{-st} \ dt $$
$$=\frac{1}{s}F(s)$$
途中計算には部分積分を利用しました。
練習問題
練習問題にチャレンジしてみましょう。ラプラス変換は慣れなので、練習問題を何回も解きなおすことをおすすめします。
(1)$L[3t^3+5t^2+4t+1]$を求めよ
ラプラス変換は多項式のとき、線形法則を利用して式を分けることが定石です。これより
$$L[3t^3+5t^2+4t+1]=L[3t^3]+L[5t^2]+L[4t]+L[1]$$
ここで$\ L[t^n]=\frac{n!}{s^{n+1}}$を利用します。この公式にn=3,2,1,0を代入することで、それぞれ
$$L[t^3]=\frac{3!}{s^{3+1}}=\frac{6}{s^4}$$
$$L[t^2]=\frac{2!}{s^{2+1}}=\frac{2}{s^3}$$
$$L[t]=\frac{1!}{s^{1+1}}=\frac{1}{s^2}$$
$$L[1]=\frac{0!}{s^{0+1}}=\frac{1}{s}$$
となります。したがって
$$=3・\frac{6}{s^4}+5・\frac{2}{s^3}+4・\frac{1}{s^2}+\frac{1}{s}$$
$$=\frac{18}{s^4}+\frac{10}{s^3}+\frac{4}{s^2}+\frac{1}{s}$$
(2)$L[e^{2t}+\sin{2t}+3\cos{t}]$を求めよ
多項式であるのでまず式を分けましょう。
$$L[e^{2t}+\sin{2t}+\cos{t}]=L[e^{2t}]+L[\sin{2t}]+L[3\cos{t}]$$
ここで$ \ L[e^{\alpha t}]=\frac{1}{s-\alpha}$、$ \ L[\sin{\omega t}]=\frac{\omega}{s^2+\omega^2}$、$ \ L[\cos{\omega t}]=\frac{s}{s^2+\omega^2}$を利用します。したがって
$$=\frac{1}{s-2}+\frac{2}{s^2+2^2}+3・\frac{s}{s^2+1^2}$$
$$=\frac{1}{s-2}+\frac{2}{s^2+4}+\frac{3s}{s^2+1}$$
(3)$L[e^{3t}\cos2t]$を求めよ
$L[ e^{\alpha t}f(t)]=F(s-\alpha)$を利用します。そのためにまず$e^{3t}$は無視して$L[\cos2t]$を求めてみましょう。
$$L[\cos2t]=\frac{s}{s^2+2^2}=\frac{s}{s^2+4}$$
これがF(s)となります。よって$L[ e^{\alpha t}f(t)]=F(s-\alpha)$よりこのF(s)を3だけ平行移動したものが答えとなります。したがって
$$L[e^{3t}\cos2t]=\frac{s-3}{(s-3)^2+4}$$
(4)$f(0)=0,f'(0)=2$のとき$L[2f^{\prime\prime}]$を求めよ
$ \ L[{f^{\prime\prime}(t)}]=s^2F(s)-sf(0)-f'(0)$を利用します。よって
\begin{eqnarray} L[2f^{\prime\prime}]& &=2・(s^2F(s)-sf(0)-f'(0))\\& &=2s^2F(s)-2sf(0)-2f'(0) \end{eqnarray}
したがって初期条件より
$$=2s^2F(s)-4$$
まとめ
今回はラプラス変換の基礎について解説しました。ラプラス変換は一見難しそうですが、慣れたらそう難しくはありません。問題演習を繰り返してラプラス変換に慣れていきましょう。


