今回の記事ではオイラー・ラグランジュ方程式(ラグランジュの運動方程式)について解説していきます。
オイラー・ラグランジュ方程式(ラグランジュの運動方程式)とは
束縛がなく、保存力のみが働くN個の独立な力学変数$q_i(t)$で構成される(自由度がN)力学系を考えます。この力学系の運動方程式を式で表したものがオイラー・ラグランジュ方程式です。このことからラグランジュの運動方程式とも呼ばれます。オイラー・ラグランジュ方程式は以下のような式です。
$$\frac{\partial L}{\partial q_i}-\frac{d}{dt}\frac{\partial L}{\partial \dot {q_i}}=0 \quad (i=1,2,…N) $$
ラグランジアンと同様に$q_i$と$\dot {q}_i$は独立な変数して扱います。
オイラー・ラグランジュ方程式とニュートンの運動方程式のつながり
位置ベクトル$x(t)$を座標としたオイラー・ラグランジュ方程式
$$\frac{\partial L}{\partial x_i}-\frac{d}{dt}\frac{\partial L}{\partial \dot {x}_i}=0 \quad (i=1,2,…3N) $$
と、ニュートンの運動方程式
$$m_i \frac{d^2 x_i}{dt^2}=F_i \quad (i=1,2,…3N)$$
は同じものを示しています。(位置ベクトル$x(t)$は三次元デカルト座標であるので、力学変数は3N個となります。)このことを確かめてみましょう。
3次元空間におけるポテンシャルエネルギー$U(x)$下の質量mの1質点系(1個の物体)を考えます。この場合のラグランジアンは$L=T-U$より、
$$L(x(t),\dot{x}(t))=\frac{1}{2}m\dot{x}(t)^2 -U(x(t))$$
ここでラグランジュ方程式を立てるために、$\frac{\partial L}{\partial x_i},\frac{d}{dt}\frac{\partial L}{\partial \dot{x}_i}$を計算していきます。$x_i$と$\dot {x}_i$は独立な変数として扱うことに注意しましょう。
\begin{eqnarray} \frac{\partial L}{\partial x_i}& &=\frac{\partial}{\partial x_i}(-U(x))\\& &=-\frac{\partial U(x)}{\partial x_i} \end{eqnarray}
\begin{eqnarray} \frac{d}{dt}\frac{\partial L}{\partial \dot{x}_i}& &=\frac{d}{dt}(\frac{\partial}{\partial \dot{x}_i} \frac{1}{2}m\dot{x}^2)\\& &=\frac{d}{dt}(m\dot{x})\\& &=m\ddot{x} \end{eqnarray}
これらをオイラー・ラグランジュ方程式$\frac{\partial L}{\partial x_i}-\frac{d}{dt}\frac{\partial L}{\partial \dot {x}_i}=0$に代入します。
$$-\frac{\partial U(x)}{\partial x_i} -m\ddot{x} =0$$
$$m\ddot{x}=-\frac{\partial U(x)}{\partial x_i}$$
これをベクトル記号で表すと
$$m\ddot{x}=-\nabla{U(x)}$$
となります。$\nabla$はベクトルの微分演算子です。これはニュートンの運動方程式に他ならないので、オイラー・ラグランジュ方程式とニュートンの運動方程式が同じものを示していることを確かめることができました。
ニュートン力学(古典力学)を飛ばして解析力学を勉強してる人の中には、なぜ$m\ddot{x}=-\nabla{U(x)}$がニュートンの運動方程式であるのか分からない人も多いと思います。そこで、高校物理の知識で問題を考えてみます。
地面から高さhにある質量mの球を、地表を基準点Oとして、垂直方向をx軸とした問題を考えてみます。この問題は以下のように図示されます。
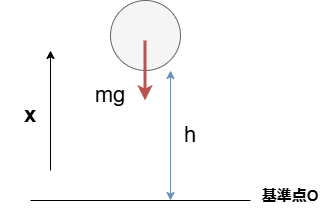
この図においてのニュートン運動方程式は、加速度を上向きが正とすると
$$ma=-mg$$
となりますね。ここで右辺を少し変形することで
$$ma=-\frac{d}{dh}\{\int_0^h mg \ dx \}$$
となります。
ここで、$\int_0^h mg \ dx=mgh$であり、これは位置$x=h$における位置エネルギー$U(h)$と一致します。これを一般化することで、位置xにおける位置エネルギー$U(x)$について
$$ma=-\frac{d}{dx}(U(x))$$
が成り立つことが予想され(一般化を根拠なしに行ったので正確な証明ではない)、これをベクトル形式で表すことで
$$m\ddot{x}=-\nabla{U(x)}$$
となり、先ほどと同じ式ができました。
練習問題
いろいろな力学系に対してオイラー・ラグランジュ方程式を使い、これがニュートンの運動方程式を再現するか確かめてみましょう。
【練習問題 1】自由落下
一様な重力場の下、自由落下している質量mの質点の運動を考える。
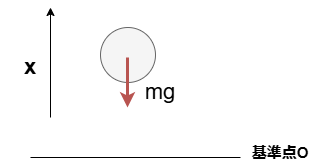
(1)位置を$x(t)$としてラグランジアンを求めよ。
(2)この系のオイラー・ラグランジュ方程式を求めよ。
【解答】
(1) この系において
$$T=\frac{1}{2}m\dot {x}^2, \quad U=mgx$$
なので、ラグランジアンの式$L=T-U$より
$$L=\frac{1}{2}m\dot {x}^2-mgx$$
(2) $L=\frac{1}{2}m\dot {x}^2-mgx$より、オイラー・ラグランジュ方程式を考えます。$x$と$\dot {x}$は独立な変数として扱うことに注意しましょう。
\begin{eqnarray} \frac{\partial L}{\partial x}& &=\frac{\partial}{\partial x}(-mgx)\\& &=-mg \end{eqnarray}
\begin{eqnarray} \frac{d}{dt}\frac{\partial L}{\partial \dot{x}}& &=\frac{d}{dt}(\frac{\partial}{\partial \dot{x}} \frac{1}{2}m\dot{x}^2)\\& &=\frac{d}{dt}(m\dot{x})\\& &=m\ddot{x} \end{eqnarray}
これらをオイラー・ラグランジュ方程式$\frac{\partial L}{\partial q_i}-\frac{d}{dt}\frac{\partial L}{\partial \dot {q_i}}=0$に代入します。
$$-mg-m\ddot{x}=0$$
$$m\ddot{x}=-mg$$
これでオイラー・ラグランジュ方程式を求めることができました。これは確かにニュートンの運動方程式を再現していますね。
【練習問題 2】単振り子
振動している単振り子がある。このとき棒の先につけた質量mの質点の運動を考える。ただし棒は伸縮せず質量はないものとする。
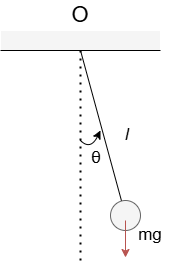
(1)棒が鉛直線となす角度を$\theta (t)$としてラグランジアンを求めよ。
(2)この系のオイラー・ラグランジュ方程式を求めよ。
【解答】
(1) 単振り子の重りの速さは$v=l\dot {\theta}$です。ここで単振り子の最下点を基準点($U=0$)とすると、この系において
$$T=\frac{1}{2}ml^2 \dot {\theta}^2, \quad U=mgl(1-cos{\theta} )$$
なので、ラグランジアンの式$L=T-U$より
$$L=\frac{1}{2}ml^2 \dot {\theta}^2-mgl(1-cos{\theta} )$$
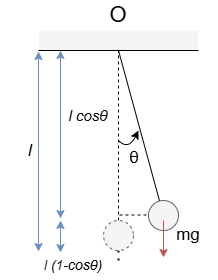
(2) $L=\frac{1}{2}ml^2 \dot {\theta}^2-mgl(1-cos{\theta} )$より、オイラー・ラグランジュ方程式を考えます。$\theta$と$\dot {\theta}$は独立な変数として扱うことに注意しましょう。
\begin{eqnarray} \frac{\partial L}{\partial \theta}& &=\frac{\partial}{\partial \theta}(mgl\cos{\theta})\\& &=-mgl\sin{\theta} \end{eqnarray}
\begin{eqnarray} \frac{d}{dt}\frac{\partial L}{\partial \dot{x}}& &=\frac{d}{dt}(\frac{\partial}{\partial \dot{x}} \frac{1}{2}ml^2 \dot {\theta}^2)\\& &=\frac{d}{dt}(ml^2 \dot{\theta})\\& &=ml^2 \ddot{\theta} \end{eqnarray}
これらをオイラー・ラグランジュ方程式$\frac{\partial L}{\partial q_i}-\frac{d}{dt}\frac{\partial L}{\partial \dot {q_i}}=0$に代入します。
$$-mgl\sin{\theta}-ml^2 \ddot{\theta}=0$$
$$ml^2 \ddot{\theta}=-mgl\sin{\theta}$$
これでオイラー・ラグランジュ方程式を求めることができました。これは確かにニュートンの運動方程式を再現していますね。
まとめ
今回はオイラー・ラグランジュ方程式(ラグランジュの運動方程式)について解説しました。この先何度も出てくるとても重要な式なので、しっかり理解しておきましょう。


