今回の記事では、一般化運動量と循環座標について解説していきます。
一般化運動量とは
ラグランジュ形式では、座標変数の設定の自由度が高く、複雑な問題を座標を適切に選ぶことによって、容易にすることができます。
この座標に運動量を選ぶとき、この一般化された運動量を一般化運動量といいます。一般化運動量の定義は以下の通りです。
力学変数$q_i$をもつ系において、$q_i$に対応した($q_i$に共役の)運動量を一般化運動量$p_i$という。
一般化運動量$p_i$はラグランジアン$L(q(t),\dot{q}(t),t)$に対して以下の式が成り立つ。
$$p_i=\frac{\partial L}{\partial \dot{q}_i}$$
エネルギー$E$を一般化運動量$p_i$を用いて表すことができます。この時の式は以下の通りです。
$$E=p_i \dot{q}_i-L$$
一般化運動量は特にハミルトン形式で重要になってきます。
循環座標とは
循環座標の定義は以下の通りです。
ラグランジアン$L(q_N,\dot{q}_N,t)$がある力学変数$q_A$に依存していない場合($\dot{q}_A$は含む)
このときの$q_A$を循環座標という。
つまり、わかりやすく言うと
$$L=L(q_1,…,q_N \ ,\dot{q_1},…,\dot{q}_N)$$
において、$q_A$は含まず、$\dot{q}_A$は含むときのことです。
ラグランジアンに循環座標があるときは、系に対称性があり、何らかの保存則が成り立ちます。
循環座標と一般化運動量の保存
先ほど述べた通り、ラグランジアンに循環座標があるときは、系に対称性があり、何らかの保存則が成り立ちます。ここで、ラグランジアンに循環座標$q_A$があれば、これに対応した一般化運動量$p_A$は保存されます。
このことをオイラー・ラグランジュ方程式$\frac{\partial L}{\partial q_i}-\frac{d}{dt}\frac{\partial L}{\partial \dot {q_i}}=0$と一般化運動量の定義$p_i=\frac{\partial L}{\partial \dot{q}_i}$より導いていきます。
\begin{eqnarray}\frac{dp_A}{dt}& &=\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_A}\\& &=\frac{\partial L}{\partial q_A}\\& &=0 \end{eqnarray}
よってラグランジアンが循環座標を持つとき、一般化運動量は保存されることが示せました。
練習問題
練習問題にチャレンジしてみましょう。
一様な重力場の下、$xy$平面を移動している質量$m$の質点の運動を考える。
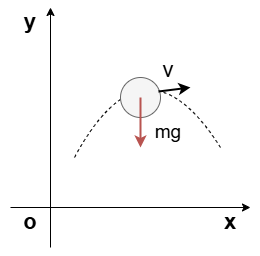
(1) 循環座標$q_A$を示せ
(2)一般化運動量$p_i$を求めよ
【解答】
(1) $xy$平面を移動する進行方向に平行な速さ$v$は、$x$軸方向への速さ$v_x$,$y$軸方向への速さ$v_y$とすると
$$v^2={v_x}^2+{v_y}^2$$
が成り立ちます。したがってこの系において
$$T=\frac{1}{2}m(\dot {x}^2+\dot{y}^2), \quad U=mgy$$
なので、ラグランジアンの式$L=T-U$より
$$L=\frac{1}{2}m(\dot {x}^2+\dot{y}^2)-mgy$$
よってこの系のラグランジアンは
$$L=L(y,\dot{x},\dot{y})$$
であり、$\dot{x}$が含まれるのに$x$が含まれていないので、 $x$が循環座標であることがわかります。
(2) 一般化運動量の定義$p_i=\frac{\partial L}{\partial \dot{q}_i}$を利用します。
$$p_x=\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$
循環座標$x$を持つことより、$x$に対応した一般化運動量$p_x=m\dot{x}$は保存します。
まとめ
今回は一般化運動量と循環座標について解説しました。これから先何度も出てくる用語なので、しっかり覚えておきましょう。


