今回の記事では同次形について解説していきます。変数分離形の知識を使うので忘れている方は以下の記事を参照してください。

同次形とは
次の形の微分方程式を同次形といいます。
$$\frac{dy}{dx}=f(\frac{y}{x})$$
つまり$\frac{dy}{dx}$=($\frac{y}{x}$だけの関数)の形です。もちろん$\frac{x}{y}$も$\frac{y}{x}$だけの関数に含まれます。
同次形の解き方
同次形の微分方程式は以下の3STEPで解くことができます。
$u=\frac{y}{x}$とおいて、$y=xu$と変形します。そのあとこの式の両辺をxで微分することで$\frac{dy}{dx}=u+x\frac{du}{dx}$$とします。
STEP1で求めた$\frac{dy}{dx}$を与式に代入します。こうすることで与式が変数分離形となります。
変数分離系を解いていきます。最後にuをもとの式に戻すことをわすれないでください。
この3STEPを使って例題にチャレンジしてみましょう。
【例題(1)】$x\frac{dy}{dx}=x+y$を解け
まずは同次形の基本形に直しておきましょう。両辺を$x$でわると
$$\frac{dy}{dx}=1+\frac{y}{x} \quad (1)$$
ここで$u=\frac{y}{x}$とおくと、$y=xu$であることより両辺をxで微分すると、積の微分法より
$$\frac{dy}{dx}=u+x\frac{du}{dx}$$
この式を(1)に代入すると
$$u+x\frac{du}{dx}=1+u$$
$$x\frac{du}{dx}=1$$
これで変数分離形になりました。次に変数分離を行います。
$$du=\frac{1}{x} \ dx$$
これで変数分離が完了しました。次に両辺をそれぞれの関数で積分します。
$$\int du=\int \frac{1}{x} \ dx$$
$$u=\log{|x|}+C_1$$
今回の定数は$C_1$なので$C=C_1$として
$$u=\log{|x|}+C$$
最後にuをもとの式に戻します。
$$\frac{y}{x}=\log{|x|}+C$$
$$y=x\log{|x|}+Cx$$
これで微分方程式を解くことができました。
同次形に帰着させて微分方程式を解く
置き換えで同次形に帰着できる形
$$\frac{dy}{dx}=f(\frac{ax+by+c}{px+qy+r})$$
この形はよく出てくるので覚えておきましょう。
同次形に帰着する解き方
$\frac{dy}{dx}=f(\frac{ax+by+c}{px+qy+r})$の形の微分方程式は$aq-bp =0$の場合と$aq-bp \neq 0$の場合で解き方が違います。それぞれ$aq-bp =0$の場合は変数分離形に帰着させて解き、$aq-bp \neq 0$の場合は同次形に帰着させて解きます。
$aq-bp =0$の場合
$aq-bp =0$の場合とはどういうときかというと、例えば与式が$\frac{dy}{dx}=\frac{4x+2y+1}{2x+y-1}$のとき
$$\frac{dy}{dx}=\frac{2(2x+y)+1}{(2x+y)-1}$$
とすることでxとyの共通の項(2x+y)が現れます。こういうときが$aq-bp =0$の場合であり、このときは変数分離形に帰着することで以下の4STEPで簡単に解くことができます。
分子か分母において共通の項の係数が小さいほうをuとします。先ほどの例でいうと、共通の項(2x+y)の係数が小さいほうは分母なので、$u=2x+y-1$とおきます。
置き換えた式の両辺をxで微分したあと、$\frac{dy}{dx}=~$の形にします。
STEP2で求めた$\frac{dy}{dx}$を与式に代入することで、与式はxとuの変数分離形となります。これを解きます。
uはあくまでも置き換えなので最後に元の式に戻すことを忘れないでください。
この4STEPを使って例題にチャレンジしてみましょう。
【例題(2)】$\frac{dy}{dx}=\frac{6x-3y+1}{2x-y+1}$を解け
$\frac{dy}{dx}=f(\frac{ax+by+c}{px+qy+r})$の形の微分方程式であり
$$\frac{dy}{dx}=\frac{3(2x-y)+1}{(2x-y)+1}$$
とすることでxとyの共通の項(2x-y)が現れるので、$aq-bp =0$の場合であることより、変数分離形に帰着させて解きます。分子か分母において共通の項(2x-y)の係数が小さいのは分母なので、$u=2x-y+1$とおきます。この式の両辺をxで微分します。
$$\frac{du}{dx}=2-\frac{dy}{dx}$$
$$\frac{dy}{dx}=-\frac{du}{dx}+2$$
これを与式に代入すると
\begin{eqnarray} -\frac{du}{dx}+2& &=\frac{3(2x-y+1)-2}{2x-y+1}\\& &= \frac{3u-2}{u}\\& &=3-\frac{2}{u} \end{eqnarray}
これで変数分離形にになりました。ここで変数分離を行います。
$$-\frac{du}{dx}=1-\frac{2}{u}$$
$$\frac{du}{dx}=\frac{2-u}{u}$$
$$\frac{u}{2-u} \ du=dx$$
次に両辺を積分します。
$$\int \frac{u}{2-u} \ du=\int dx$$
$$\int (-1+\frac{2}{2-u})=\int dx$$
$$-u-2\log{|2-u|}=x+C_1$$
uをもとの式に戻します。
$$-2x+y-1-2\log{|-2x+y+1|}=x+C_1$$
$$y-3x-2\log{|y-2x+1|}=C_1+1$$
今回の定数は$C_1+1$なので$C=C_1+1$として
$$y-3x-2\log{|y-2x+1|}=x+C$$
これで微分方程式を解くことができました。
$aq-bp \neq 0$の場合
$aq-bp \neq 0$の場合はどういうときかというと、先ほどの$aq-bp =0$の場合の時と違い、xとyの共通の項が現れない式のときです。このときは同次形に帰着することで以下の4STEPで解くことができます。
$ax+by+c=0$,$px+qy+r=0$として連立方程式を解いて、xとyを求めます。
STEP1で求めた解$x=\alpha$,$y=\beta$を平行移動させて、$X=x-\alpha$,$Y=y-\beta$とおきます。
\begin{eqnarray} \frac{dy}{dx}& &=\frac{dy}{dY}・\frac{dY}{dX}・\frac{dX}{dx}\\& &=1・\frac{dY}{dX}・1=\frac{dY}{dX} \end{eqnarray}
より与式をXとYの座標に変換します。これで与式は同次形となります。
同次形を解きます。最後に座標をxとyの座標に戻すことを忘れないようにしましょう。
やっていることのイメージを詳しく解説します。まず2直線$ax+by+c=0$,$px+qy+r=0$の連立方程式を解くことで、以下の図においての交点(解)$(\alpha,\beta)$を求めます。

この交点をもとに微分方程式を解いていきたいのですが、交点(解)が原点ではないため問題を解くのが難しくなってます。よって$X=x-\alpha$,$Y=y-\beta$と座標変換して、交点を平行移動することで原点と一致させます。

こうすることで問題を解決するのが容易になったため、このまま解いていきます。最後にxy座標に戻すことで微分方程式を解くことができたことになります。
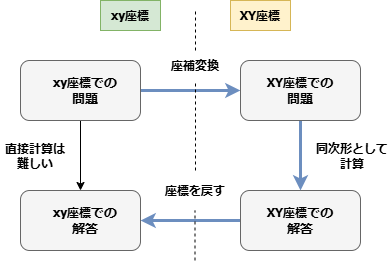
このイメージをすることで、なぜ$aq-bp =0$のとき同次系に帰着せず、いきなり変数分離形に帰着したかがわかります。$aq-bp =0$のとき下の図のように2直線は平行なので、交点ができないからです。

この4STEPを使って例題にチャレンジしてみましょう。
【例題(3)】$\frac{dy}{dx}=\frac{2x+y-5}{x-y-1}$を解け
$\frac{dy}{dx}=f(\frac{ax+by+c}{px+qy+r})$の形の微分方程式であり、xとyの共通の項が現れないので、$aq-bp \neq 0$の場合であることより、同次形に帰着させて解きます。
まずは$2x+y-5=0,x-y-1=0$の連立方程式を解きます。すると$(x,y)=(2,1)$と解が求まります。ここで平行移動を行います。よって$X=x-2,Y=y-1$とおきます。すると
\begin{eqnarray}\frac{dy}{dx}& &=\frac{dy}{dY}・\frac{dY}{dX}・\frac{dX}{dx}\\& &=1・\frac{dY}{dX}・1=\frac{dY}{dX} \end{eqnarray}
これより与式を座標変換します。
\begin{eqnarray} \frac{dY}{dX}& &=\frac{2(X+2)+(Y+1)-5}{(X+2)-(Y+1)-1}\\& & =\frac{2X+Y}{X-Y} \\& &=\frac{2+\frac{Y}{X}}{1-\frac{Y}{X}} \quad(1) \end{eqnarray}
これで同次形にすることができました。これを解いていきます。ここで$u=\frac{Y}{X}$とおくと、$Y=Xu$であることより両辺をXで微分すると、積の微分法より
$$\frac{dY}{dX}=u+X\frac{du}{dX}$$
この式を(1)に代入すると
$$u+X\frac{du}{dX}=\frac{2+u}{1-u}$$
$$X\frac{du}{dX}=\frac{2+u^2}{1-u}$$
これで変数分離形になりました。次に変数分離を行います。
$$\frac{1-u}{2+u^2} \ du=\frac{1}{X} \ dX$$
これで変数分離が完了しました。次に両辺をそれぞれの関数で積分します。
$$\int \frac{1-u}{2+u^2} \ du=\int \frac{1}{X} \ dX$$
$$\int (\frac{1}{2+u^2}-\frac{u}{2+u^2}) \ du=\int \frac{1}{X} \ dX$$
これらの積分は基本的な形なので計算は省略します。
$$\frac{1}{\sqrt{2}}\arctan{(\frac{u}{\sqrt{2}})}-\frac{1}{2}\log{(2+u^2)}=\log{X}+C_1$$
uをもとの式に戻し、定数もCに直します。
$$\frac{1}{\sqrt{2}}\arctan{(\frac{Y}{\sqrt{2} \ X})}-\frac{1}{2}\log{(2+\frac{Y^2}{X^2})}=\log{|X|}+C$$
最後に座標をxとyの座標に戻します。
$$\frac{1}{\sqrt{2}}\arctan{(\frac{y+1}{\sqrt{2}(x+2)})}-\frac{1}{2}\log{\{2+\frac{(y+1)^2}{(x+2)^2}\}}=\log{|X|}+C$$
これで微分方程式を解くことができました。
練習問題
練習問題にチャレンジしてみましょう。
(1)$x\frac{dy}{dx}=y+\sqrt{x^2+y^2}$を解け
まずは同次形の基本形に直しておきましょう。両辺を$x$でわると
$$\frac{dy}{dx}=\frac{y}{x}+\sqrt{1+(\frac{y}{x})} \quad (1)$$
ここで$u=\frac{y}{x}$とおくと、$y=xu$であることより両辺をxで微分すると、積の微分法より
$$\frac{dy}{dx}=u+x\frac{du}{dx}$$
この式を(1)に代入すると
$$u+x\frac{du}{dx}=u+\sqrt{1+u^2}$$
$$x\frac{du}{dx}=\sqrt{1+u^2}$$
これで変数分離形になりました。次に変数分離を行います。
$$\frac{1}{\sqrt{1+u^2}} \ du=\frac{1}{x} \ dx$$
これで変数分離が完了しました。次に両辺をそれぞれの関数で積分します。
$$\int \frac{1}{\sqrt{1+u^2}} \ du=\int \frac{1}{x} \ dx$$
左辺の形の積分はとても難しいです。ここでは計算は省略します。
左辺の形の積分についてわからなかった人は以下の記事の(5)に全く同じ問題があるので参照してください。

積分をすることで
$$\log{(u+\sqrt{1+u^2})}=\log{x}+C_1$$
$$u+\sqrt{1+u^2}=\pm e^{\log{x}+C_1}$$
ここで定数項をCとおきます。xがついているものは定数ではないので
$$u+\sqrt{1+u^2}=\pm e^{\log{x}}・e^{C_1}$$
として分けることで、この式において定数は$\pm e^{C_1}$なので$C=\pm e^{C_1}$とすると
$$u+\sqrt{1+u^2}=Cx$$
最後にuをもとの式に戻します。
$$\frac{y}{x}+\sqrt{1+(\frac{y}{x})^2}=Cx$$
$$y+\sqrt{x^2+y^2}=Cx^2$$
(2)$\frac{dy}{dx}=\frac{2x-2y+5}{x-y+1}$を解け
$\frac{dy}{dx}=f(\frac{ax+by+c}{px+qy+r})$の形の微分方程式であり
$$\frac{dy}{dx}=\frac{2(x-y)+5}{(x-y)+1}$$
とすることでxとyの共通の項(x-y)が現れるので、$aq-bp =0$の場合であることより、変数分離形に帰着させて解きます。分子か分母において共通の項(x-y)の係数が小さいのは分母なので、$u=x-y+1$とおきます。この式の両辺をxで微分します。
$$\frac{du}{dx}=1-\frac{dy}{dx}$$
$$\frac{dy}{dx}=-\frac{du}{dx}+1$$
これを与式に代入すると
\begin{eqnarray} -\frac{du}{dx}+1& &=\frac{2(x-y+1)+3}{x-y+1}\\& &= \frac{2u+3}{u}\\& &=2+\frac{3}{u} \end{eqnarray}
これで変数分離形にになりました。ここで変数分離を行います。
$$-\frac{du}{dx}=1+\frac{3}{u}$$
$$\frac{du}{dx}=-\frac{u+3}{u}$$
$$\frac{u}{u+3} \ du=-dx$$
次に両辺を積分します。
$$\int \frac{u}{u+3} \ du=\int -dx$$
$$\int 1-\frac{3}{u+3}=\int -dx$$
$$u-3\log{|u+3|}=-x+C_1$$
uをもとの式に戻します。
$$x-y+1-3\log{|x-y+4|}=-x+C_1$$
$$2x-y-3\log{|x-y+4|}=C_1-1$$
今回の定数は$C_1-1$なので$C=C_1-1$として
$$2x-y-3\log{|x-y+4|}=C$$
(3)$\frac{dy}{dx}=\frac{x-2y+4}{2x+y-7}$を解け
$\frac{dy}{dx}=f(\frac{ax+by+c}{px+qy+r})$の形の微分方程式であり、xとyの共通の項が現れないので、$aq-bp \neq 0$の場合であることより、同次形に帰着させて解きます。
まずは$x-2y+4=0,2x+y-7=0$の連立方程式を解きます。すると$(x,y)=(2,3)$と解が求まります。ここで平行移動を行います。よって$X=x-2,Y=y-3$とおきます。すると
\begin{eqnarray}\frac{dy}{dx}& &=\frac{dy}{dY}・\frac{dY}{dX}・\frac{dX}{dx}\\& &=1・\frac{dY}{dX}・1=\frac{dY}{dX} \end{eqnarray}
これより与式を座標変換します。
\begin{eqnarray} \frac{dY}{dX}& &=\frac{(X+2)-2(Y+3)+4}{2(X+2)+(Y+3)-7}\\& & =\frac{X-2Y}{2X+Y} \\& &=\frac{1-2\frac{Y}{X}}{2+\frac{Y}{X}} \quad (1) \end{eqnarray}
これで同次形にすることができました。これを解いていきます。ここで$u=\frac{Y}{X}$とおくと、$Y=Xu$であることより両辺をXで微分すると、積の微分法より
$$\frac{dY}{dX}=u+X\frac{du}{dX}$$
この式を(1)に代入すると
$$u+X\frac{du}{dX}=\frac{1-2u}{2+u}$$
$$X\frac{du}{dX}=\frac{1-4u-u^2}{2+u}$$
これで変数分離形になりました。次に変数分離を行います。
$$-\frac{-2-u}{1-4u-u^2} \ du=\frac{1}{X} \ dX$$
これで変数分離が完了しました。次に両辺をそれぞれの関数で積分します。
$$\int -\frac{-2-u}{1-4u-u^2} \ du=\int \frac{1}{X} \ dX$$
$$-\frac{1}{2}\log{|1-4u-u^2|}=\log{X}+C_1$$
$$\log{|1-4u-u^2|}=-2\log{|X|}-2C_1$$
$$1-4u-u^2=\pm e^{-2\log{|X|}-2C_1}$$
ここで定数項をCとおきます。xがついているものは定数ではないので
$$1-4u-u^2=\pm e^{-2\log{|X|}}・e^{-2C_1}$$
として分けることで、この式において定数は$\pm e^{-2C_1}$なので$C=\pm e^{-2C_1}$とすると
$$1-4u-u^2=CX^{-2}$$
uをもとの式に戻して
$$X^2-4XY-Y^2=C$$
最後に座標をxとyの座標に戻します。
$$x^2-4xy-y^2+8x+14y=C$$
まとめ
今回は同次形について解説しました。微分方程式の中でも頻繁に使う形なので、何回も演習を繰り返して慣れていきましょう。


