今回の記事では、仮想仕事の原理について図や実例を交えてわかりやすく解説していきます。
仮想仕事の原理とは
仮想仕事の原理とは、仮想変位(少しだけ質点を動かすこと)がする仕事である仮想仕事のする仕事は0であるという法則です。このことを表した式は以下の通りです。
$$F・δr=0$$
仮想仕事の原理の導出
ここからは、仮想仕事の原理を導いていきます。まずは1個の質点を考えます。この質点に働いているすべての力の合力をFとすると、つりあっている状態ではもちろん
$$F=0$$
です。質点を、この状態から任意の仮想的な変位
$$δr=(δx,δy,δz)$$
だけ動かします。
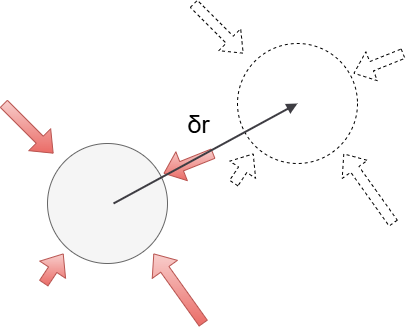
この仮想変位でFがする仕事が、仮想仕事です。F=0より、微小変位$δr=(δx,δy,δz)$との内積は
$$F・δr=0$$
を満たします。これで仮想仕事の原理を導くことができました。
仮想仕事の原理の利点
ここからは、仮想仕事の原理を使うことでどういう利点があるのかを解説していきます。仮想仕事の原理を使うメリットが大きく2つあります。
- 束縛力を無視できる
- 複数個の物体が連動しているとき問題を簡単にできる
それぞれ解説していきます。
束縛力を無視できる
仮想仕事の原理を使うことで、張力や垂直抗力などの束縛力(物体の位置を制限するようにはたらく力)を無視することができます。実例として、摩擦がない斜面に物体が糸につながれて静止しているものから、張力を求めることを考えます。
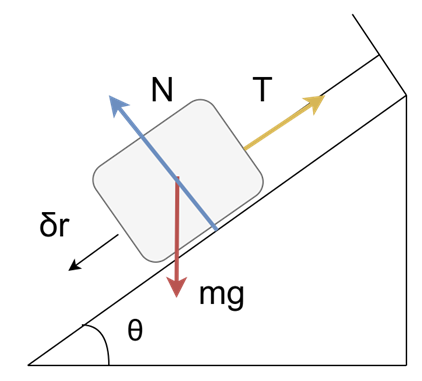
まずは、仮想仕事の原理を使わずに力のつりあいだけで求めた場合を考えます。質点が静止しているので力のつりあいの式は
$$F=N+T+mg=0$$
ですね。ここから重力を斜面に平行な成分と斜面に垂直な成分に分解して、斜面に平行な成分のつりあいを考えると
$$T=mg\sin{θ}$$
となり張力が求まりました。
次に仮想仕事の原理で求めた場合を考えます。ここで斜面に沿ってδr降りる仮想変位をとります。このとき物体に対して張力は-Tδr、重力はmgδr sinθの仕事をします。このとき仮想仕事の原理より
$$-Tδr+mgδr\sin{θ}$$
よって
$$T=mg\sin{θ}$$
となり同じく張力が求まりました。ここであることに気づきます。仮想仕事の原理を使って張力を求めたときに、この場合の束縛力である垂直抗力を全く使っていません。このように、仮想仕事の原理を使うことによって束縛力を無視することができます。
複数個の物体が連動しているとき問題を簡単にできる
仮想仕事の原理を使うことで、複数個の物体が連動しているときに物体間で媒介している力による仕事を考えなくてよくなります。実例として、定滑車につながれた2つの物体が静止しているものを考えます。
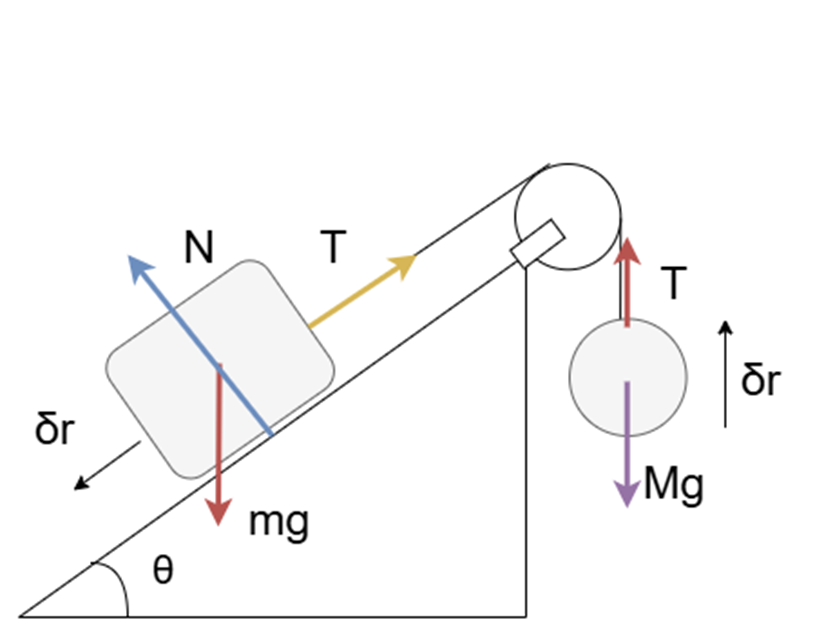
この場合、物体間で媒介している力は張力Tです。それぞれの物体はつながっているので「連動した仮想変位」δrをとります。それぞれの物体について、つりあいを考えると
$$ A \quad (mg\sin{θ}-T)δr=0$$
$$ B \quad (-Mg+T)δr=0$$
と式を立てることができます。もちろんこのときも、この場合の束縛力である垂直抗力Nは出てきません。Tδrが2つの式の両方にあることより、この2つの式をまとめると
$$(mg\sin{θ}-Mg)δr=0$$
となり、張力Tも出てこなくなりました。ここでどうせ垂直抗力Nも張力Tも出てこなくなるんだから、最初から両方無視して仮想仕事を考えてみることにします。
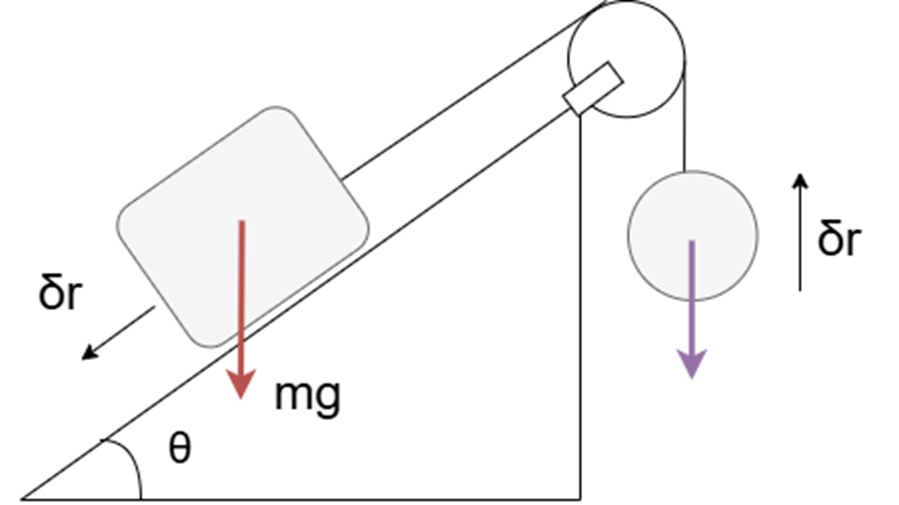
すると上の図のように重力の仮想仕事を考えるだけでいいので
$$mg\sin{θ}δr-Mgδr=0$$
という式が一気に出てきました。このように、仮想仕事の原理を複数個の物体が連動しているときに使うことで、問題を簡単にすることができます。
まとめ
今回は仮想仕事の原理について解説しました。うまく使えば問題をとても簡単にできる便利な法則です。しっかりマスターして、実際に使えるようにしましょう。


